Dès lors, nous avons pu déterminer le coefficient de traînée de chacune des formes que nous avons utilisées. Pour cela, nous avons donc utilisé la relation

      F= 1/2 x S x v² x Cx x ρ                                

      Cx = 2F/ ( S x v² x ρ )

avec chacun de nos résultats expérimentaux :

Théophile Costes

Céciles Trapp

Battistella Enzo

Accueil

Introduction

Expérience

Résultats expérimentaux

Interprétation

Algorithme

Algorithme ( algobox )

Conclusion

Lexique

Sources

Livre d'or

Interprétation

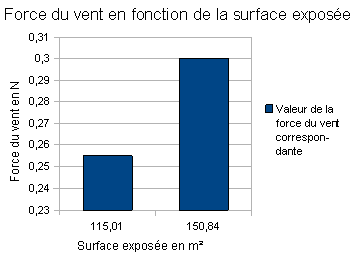
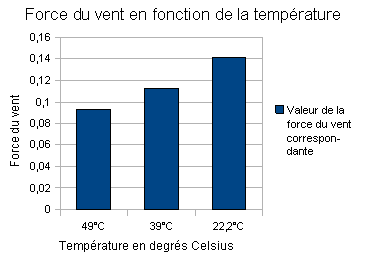
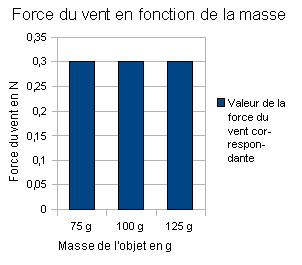
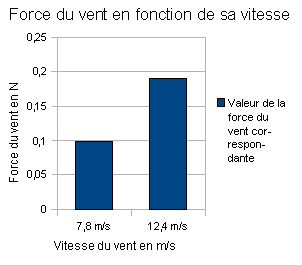
  A partir de ces résultats nous avons pu réaliser les graphiques suivants :

 

 

  De plus, pour les prismes puisque le vent est projeté sur des angles aigus (65° et 30°) le régime d'écoulement est toujours turbulent. Au vu des résultats du précédent tableau et sachant cela, dans toutes nos expériences l'air s'écoule de façon turbulente. On peut ainsi calculer le seul paramètre manquant, le coefficient de traînée, avec la relation :

F= 1/2 x S x v² x Cx x ρ

  Nous cherchons tout d'abord la masse volumique de l'air (ρ). Pour cela, nous savons grâce à la loi des gaz parfaits que

pV = RnT où p est la pression ( ici atmosphérique )en Pascals, V le volume en mètre cube, R la constante des gaz parfaits en unité du système international ( USI ), n la quantité de matière en moles et T la température en Kelvins.

pV = RnT             n/ V = p/ ( RT )

Or par définition : ρ = m/ V avec m la masse en kilogrammes. De plus, n = m/M Avec M la masse molaire moléculaire d'où

ρ = ( n x M )/ V. Ainsi, n/ V = ρ/M = p/ ( RT ) donc

ρ = ( pM )/ ( RT ). Comme M_air = 29 x 10^-3 kg/mol R = 8,31 USI et p vaut environ 10⁵ Pa, il suffit donc de calculer ρ en fonction des différentes températures de l'air de nos expériences.

  Maintenant, nous calculons la surface exposée au vent de chaque solide :

  Nous remarquons que les coefficients de traînée du cylindre et du parallélépipède restent proches au cours des différentes expériences. Afin de déterminer une valeur approchée de ce coefficient nous faisons la moyenne des résultats obtenus.        

  Ainsi :

Cx_Cylindre = ( 0,143 + 0,178 + 0,199 + 0,109 ) /4 = 0,157

Cx_{Parallélépipède} = ( 0,319 + 0,286 ) /2 = 0,303

  Nous avons ainsi déterminé que la température de l'air ( qui modifie la masse volumique de l'air ), la forme de l'objet, la vitesse du vent et la surface de l'objet ont une incidence sur la valeur de la force que le vent exerce sur l'objet conformément à nos recherches. A l'inverse la masse de l'objet n'entre pas en compte.

Ensuite, nous avons déterminé le nombre de Reynolds de chacun de nos objets pour chaque vitesse de vent à laquelle il a été soumis à l'aide de la formule Re = ( v x L ) / h expliquée précédemment. La viscosité de l'air est de 1,8 x 10^-5 Pa.s. Nous avons ainsi obtenu le tableau de valeurs suivant :

Retour en haut